|
|
Post by Herbert Blenner on Feb 11, 2019 15:17:32 GMT -5
Grading the Forensic PathologistsPosted January 12, 2011President Kennedy's entry wounds provide an opportunity to evaluate the performance of the forensic pathologists.
The pathologists from Bethesda documented the longer axis of the wound in the back of President Kennedy as roughly parallel to the long axis of the body. Commander Humes directed H. A. Rydberg in making his drawing of this wound.
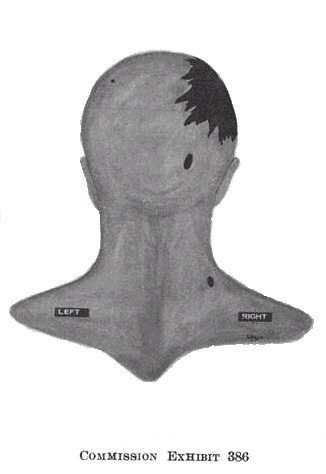
Figure 1 - Rydberg Drawing of the Back Wound
CE 386 shows the longer axis as described by Humes.
However, the forensic pathology panel presented a drawing by Ida Dox of Kennedy's back wound whose longer axis was nearly perpendicular to the long axis of the body.

Figure 2 - Dox Drawing of the Back Wound
Although the panelists explicitly noted the near perpendicularity of the longer axis of the wound to the long axis of the body, they were silent about the undeniable conflict with the description of the wound discussed and documented by Humes.
Likewise, the Bethesda pathologists did not object to the panelists who rotated the longer axis of the back wound by ninety degrees. Perhaps they were preoccupied with the scalp wound?
Humes placed the scalp wound of entry slightly to the right of the EOP while the forensic pathology panel concurred with the Clark Panel in locating the 6 mm by 15 mm elliptical scalp wound near the cowlick.
Although the panelist accepted the arguments presented by Larry Sturdivan against a 15-mm elliptical wound on Governor Connally's back, they failed to acknowledge application of the same valid arguments to the 15 mm elliptical wound of Kennedy's scalp.
So we have two documented instances where the members of the forensic pathology panel either played dumb or demonstrated their ignorance of wound analysis.
Crime scene analysts recognize the relationship between the axes of an elliptical hole or wound and the cosine of the incidence/entry angle of the bullet.
This relationship is complemented by the coincidence of the direction of the longer axis of an elliptical wound with the tangential component of the striking velocity of the bullet.
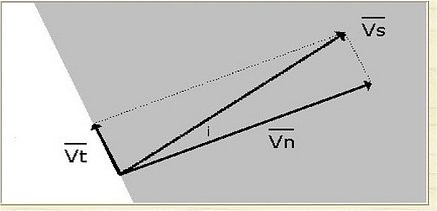
Figure 3 - Tangential and Normal Components of Velocity
So forensic analysts have tools to determine the direction of an entering or exiting bullet from the dimensions of an elliptical or oval wound. The failure of pathologists of the Clark and the HSCA Medical panels to use these relationships strongly suggests that they lacked the caliber to apply mathematics to a physical problem. In fact, the Summary of the Forensic Pathologist' Perspective on Wound Ballistics shows that those medical professionals did not have the background to solve grade school science problems.
|
|
|
|
Post by Herbert Blenner on Feb 11, 2019 15:20:12 GMT -5
Critique of the Forensic Pathologistsby Herbert Blenner | Posted May 16, 2011Forensic Pathologists are medical specialists who deal with the legal aspects of injury or death. By their medical training these specialists are not necessarily equipped to analyze the mechanism of wounding. Instead they use their experience to suggest likely explanations but seldom state definitive conclusions. Their uncertainty arises from ignorance of applied mathematics and physics.
The following quotations from the "Summary of the Forensic Pathologists’ Perspective of Wound Ballistics" published by the HSCA show that the forensic pathologists of the FPP were unprepared to analyze the wounds inflicted upon President Kennedy and Governor Connally.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 163
(417) A missile must have sufficient velocity (speed) to cause a particular wound. The velocity depends on the type of ammunition employed, including the type of powder and powder charge. Velocity drops off as the distance between the weapon and the target increases.
Speed is not a synonym of velocity. A velocity is a speed and a direction. This direction requires two additional measures. These measures may be any combination of an angle or another speed in a specified direction. So by calling a speed a velocity the ballistics community conceals its neglect of the directional nature of velocity.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 164
(423) Wound ballistics research has shown that a missile velocity of 125 to 170 feet per second is necessary for penetration of the human skin when using steel spheres varying from one-sixteenth to one quarter inch in diameter. Clothing also impairs perforation, but it usually less efficient than skin in hindering penetration, depending on its nature.
A missile has a threshold velocity for penetration into an obstacle. This velocity has a threshold speed and a special direction that is perpendicular to the obstacle at the point of impact.

Every striking velocity, Vs, can be resolved into a normal velocity, Vn, perpendicular to and directly into the surface of the struck object and a tangential velocity, Vt, parallel to the surface of the object. When the tangential component of the velocity is considerable, they describe the strike as tangential. Alternately the expression at normal incidence refers to a strike where a minute angle between the striking velocity and the normal velocity renders the tangential velocity negligible. This terminology recognizes the angle between the striking and normal velocities as the incidence angle, i.
Familiar trigonometric functions of the incidence angle relate the components of the striking velocity. In particular the tangential speed, Vt, equals the striking speed, Vs, multiplied by the sine of the incidence angle, i. Correspondingly the normal speed, Vn, equals the striking speed, Vs, multiplied by the cosine of the angle of incidence. The form of the latter relationship is suited to determine the smallest striking speed or the largest incidence angle for the normal speed of a missile to exceed the threshold speed for penetration, Vp, of the object. In symbols the condition for penetration becomes Vs cos ( i ) > Vp.
Suppose the threshold for penetration of skin is 150 fps and a missile strikes with a speed of 750 fps. The penetration condition gives cos ( i ) > 1/5. So the missile will penetrate the skin if its incidence angle is less than arccos (1/5) or 78.5 degree. Alternately if the incidence angle is greater than 78.5 degree then the missile would deflect without penetration of the skin. This example shows that resolving a striking speed into normal and tangential speeds facilitates solution of the penetration or the deflection problem.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 164
(423) . . . The size of the defect in the skin varies considerably depending on the size and velocity of the missile. Skin is extremely elastic; it often stretches considerably to allow missile penetration and then returns to its normal shape thereafter, leaving a defect smaller than the missile itself. Close proximity of the weapon to the skin or bone beneath the skin and the angle of impact may enlarge the entrance perforation.
The size of the defect on and beneath the surface is strongly dependant upon the yaw angle of the striking missile. For a bullet with a diameter of 6.5 mm and length of 30 mm the striking or displacement area of the missile varies by a factor of 5.9 with changes in yaw angle.
The impact angle between the direction of the entering missile and the parallel to the skin always affects the size of the surface wound without changing the size of the wound immediately beneath the surface. This effect arises since distance along the wound track contributes toward elongation of one dimension of the surface wound.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 164
(424) The characteristics of the abrasion collar surrounding the entrance perforation reflect the direction of the bullet at the instant of impact with the skin and the angle of the trajectory prior to contact with the skin, as well as the shape of the missile itself. If the trajectory is perpendicular to the surface of the skin, the hole is usually round and the abrasion collar correspondingly symmetrical around it.
The opening sentence makes three claims. It relates the direction of the striking bullet to the characteristics of the abrasion. This claim is vague since they did not specify that the reflected direction is relative to the angular orientation of the victim. The second assertion is wrong since the characteristics of the abrasion convey no information that relates the orientation of the victim to the trajectory angles of a bullet in flight. The third claim is correct.
Although the second sentence is correct, it is misleading in that a round hole always reflects entry by a bullet whose direction was perpendicular to the surface of the skin at the point of entry. Under these circumstances the surrounding abrasion is usually symmetric about the hole with the symmetry of the abrasion being contingent upon the uniformity of tissues immediately surrounding the round hole.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 165
(424) . . . If the angle of the trajectory of the missile to the skin surface is other than perpendicular, the abrasion collar may be asymmetrical, that is, more prominent on the surface with the most acute angle between the skin and the bullet, and less apparent on the opposite surface, where there may be undermining of the tissues. (See fig. 46 showing an abrasion collar produced by a missile striking at an acute area.)

Figure 2 - Undermining of tissues
When the abrasion collar is oval or elliptical it surrounds an elliptical entrance perforation and shows that the trajectory of the bullet was not perpendicular to the surface of the skin. Since an elliptical abrasion collar has two axes of symmetry, it lacks a prominent portion. However, an oval abrasion collar with one symmetry axis has an asymmetry and a more prominent portion. So an oval abrasion collar always has its more prominent portion nearer the side of the wound with the most acute angle and undermining on the opposite side.
Undermine of the skin occurs with every tangential entry and becomes increasingly pronounced with increasing incidence angle. Reading "Undermining of tissues" from left to right shows three tangential entries with incidence angles of 20, 40 and 60 degree. The lightly shaded triangular regions immediately to the left of the wound tracks represent cross sections of undermined tissues. The undermining is most pronounced along the major axis of the bullet hole, becomes less pronounced along directions between the major and minor axes and vanishes at all directions bounded by the minor axis and the portion of the major axis that made an acute angle with the trajectory of the bullet.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 166
(425) If a missile strikes an intervening target, its normal yaw may be exaggerated, or it may begin to tumble. The entry wound in subsequent target might reflect this distortion in trajectory by anything from a very slight asymmetry to an ovoid or virtually rectangular reentry wound. The latter would be the case if the missile were to strike sideways and is somewhat similar to what was described in some of the initial medical reports on the wound in the posterior thorax of Governor Connally. (See fig. 47 a drawing showing yawing or tumbling.)
In perhaps the most outrageous obstruction of understanding published by the House Select Committee on Assassinations, the Forensic Pathology Panel presented a graphic entitled, " Figure 46. - Drawing of a typical entry wound, displaying an asymmetrical abrasion collar from a distant rifle shot with a trajectory at an acute angle to the skin surface." Their graphic combined a wildly tumbling bullet entering a target at normal incidence with an oval abrasion surrounding an elliptical hole. The panel complemented their contradictions of these fundamentals of forensic analysis in their following graphic labeled, " Figure 47. - Drawing of an entry wound caused by a tumbling or yawing missile." This graphic showed a bullet with negligible yaw entering a target with a considerable incidence angle and an oval abrasion surrounding a rectangular hole with rounded corners.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 167
(426) A missile’s path may also be deflected from a true straight line by striking an intervening target, with the extent of deflection usually based on the mass of the intervening object.
Newton’s law of motion shows that the change in action from the force exerted by the target determines the change in momentum of the missile. When the direction of the action or force is opposite the direction of the missile, slowing without deflection occurs. However, a tangential strike by the missile upon a solid target causes the direction of the action to differ from the direction of the missile. So deflection begins at first contact and ceases when crushing reforms the surface of the target to mate with the penetrating missile. The duration of a tangential strike is usually extremely brief and renders negligible the action from a considerable force. A grazing collision in which the missile impinges the target without breaking the surface overcomes the extreme brevity of the more common type of tangential collision. So a grazing collision may deflect a medium speed missile by several degrees.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 167
(427) The accuracy of a weapon is provided by the spin imparted by the rifling within the weapon and, to a lesser degree, the shape of the projectile. An elongated, symmetrically shaped missile is a more accurate than an irregular or spherical one. Other considerations in accuracy are distance to the target, effect of gravity on the missile while in flight, and effects of air resistance. Air resistance varies considerably with the speed of the missile. A very high velocity missile, after leaving the weapon, losses its speed at a much greater rate than does a low or intermediate velocity missile.
The speed imparted to the missile by the barrel is the primary factor is determining the accuracy of a weapon. A higher speed reduces the flight time during which gravitational and aerodynamic forces act to degrade accuracy. Shaping a missile to reduce the area of its windward surface improves accuracy by reducing its rate of slowing while imparting a spin to a radially symmetric and elongated missile assists in holding the area of its windward surface to a minimum.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 167
(428) A missile's pathway from the weapon to the target is known as its trajectory. A bullet should travel only a short distance after leaving the barrel before it stabilizes, minimizing the tendency to yaw. During the first hundred yards or so, the bullet yaws periodically, with its tip oscillating slightly from the line of flight. While in flight, the bullet’s movement, although much quicker because of its high rate of spin, mimics that of a spinning top. At one instant the bullet is point on, at the next its axis is at a slight angle to the line of flight. These motions are periodic. This angle of yaw increases to a certain degree and then progressively decreases until it is again zero, whereupon another similar gyration commences.
The tip of a wobbling bullet as seen from a chasing that keeps the same distance from the missile traces out an inward spiral as the azimuthal angle of the bullet rotates three hundred sixty degrees for a distance equal to the length of the final full twist of the rifle. Simultaneously the yaw angle slowly decreases as the spinning bullet adjusts its axis of spin imparted by the rifle to an intrinsic axis determined by its shape. These transient motions die out as the stable missile travels several hundred feet. Photographing these motions with the line of flight in the plane of view produces the reported illusion of an oscillating yaw angle.
External forces drive a gyrating top while internal forces wobble the bullet. So the analogy to a gyrating top is wrong.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 168
(428) . . . The tendency to yaw increases in proportion to the density of the medium through which the missile passes relative to air; in tissues it may be increased many times more than in air (approximately 800), resulting in rapid, complex bullet motions.
The opposing force upon the bullet is proportional to the density of a liquid or a gaseous medium. For a solid such as tissue this opposing force is unrelated to density and depends upon the dynamic yield strength of the medium. Further the "tendency to yaw" properly measured by the torque is a function of the moment arm between the bullet’s center of gravity and the point of action of the opposing force, the magnitude of the opposing force, and the sine of the angle between the moment arm and the opposing force. The torque equals the vector product of the moment arm and the opposing force.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 168
(429) . . . Bone or other extremely dense tissue, such as cartilage, in the immediate pathway of the missile might alter the angle of the track through the body after the characteristic skin perforation. This alteration is distinguishable from that produced by yaw, which, at a particular point in the passage through the body, might cause the missile to be out of line with its pathway, although the pathway itself remains straight.
The path of a missile with yaw, a misalignment between its long axis and forward direction of motion, curves toward the unchanging direction of its long axis. This deflection reduces the yaw angle and eventually the missile resumes a straight path following the direction of its long axis. They call this the airfoil effect.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 168
(430) The panel believes that the difficulty which Drs. Humes, Finck, and Boswell experienced in trying to place a soft probe through the bullet pathway in President Kennedy's neck probably resulted from their failure or inability to manipulate this portion of the body into the same position it was in when the missile penetrated. Rigor mortis may have hindered this manipulation. Such placement would have enabled reconstruction of the relationships of the neck and shoulder when the missile struck. It is customary, however, to dissect missile tracks to determine damage and pathway. Probing a track blindly may produce false tracks and misinformation.
A bullet stretches a tissue to its breaking point immediately before penetration. This physically obvious fact causes no problem for probing a wound when the missile crossed the boundary between differing tissues at close to a right angle. In this case, elastic relaxation and swell of tissues after passage of the bullet do not change the alignment of tissues on opposite sides of the boundary.

Figure 3 - Disconnected Wound Track
When the bullet tangentially crosses a boundary with slippage, it stretches the tissues in a direction parallel to the boundary. Now elastic relaxation of the tissues will misalign and may disconnect the wound track. Under these circumstances a probe must stretch tissues to their breaking points to realign the wound track.
Referring to figure three white represents the wound track and dark grey shows a less compliant tissue beneath a more compliant tissue represented by light grey. As the missile penetrates it laterally stretches the more compliant tissue farther than the less compliant tissue. At this instant the wound tracks align. However, after passage of the bullet both tissues relax in proportion to their stretches during penetration. The more compliant tissue moves farther than the less compliant tissue. This mechanism will misalign and may disconnect the wound tracks.
Differences of the elastic compliances of tissues on opposite sides of the boundary encourage disconnection of the wound track while density of the tissues and speed of the missile discourage this effect.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 168
(431) The panel is concerned as to the degree of accuracy attainable in determining the missile trajectory based on backward extension of a bullet track from within the body, Particularly if precision within the range of a few degrees is required. An intermediate or high velocity bullet creates a temporary [sic] bullet track relatively larger than that of the bullet itself. This precludes reconstruction within the required degree of accuracy.
The backward extension method makes two assumptions. The first assumption being that a missile track connects both wounds and the second assumption is straightness of the connecting track. Applying the backtrack method without verifying these assumptions is unscientific.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 169
(434) The determination of the point of origin of a missile by backward extension from a bullet track through a body must take into account not only the above variable factors, but also requires knowing, reasonably precisely, the exact position of that portion of the body penetrated at the instant it was struck. Any motion of the body, no matter how slight, would alter the extended trajectory of the missile from the bullet track in the body considerably and thereby change the point of origin. The longer the distance of the trajectory, the greater the magnification of even the smallest error in determining body position or path in the body.
The determination of the point of origin of a missile by the backward extension or the striking angle method requires knowledge of the angular orientation, not the position, of the victim when shot.
When the missile makes an elliptical wound of entry such as President Kennedy’s entry wounds or Governor Connally’s back wound then the analysis does not depend upon the motion of the victim during transit of the missile or the size or straightness of the internal wound track. Under these conditions the dimensions of the wound enable calculation of the incidence angle of the striking bullet to within a few degrees. This level exceeds the accuracy of determining the posture of the victim when shot. So the determination of the missile trajectory is limited by knowledge of the posture of the victim when shot.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 169
(435) In the panel members’ experience, if a missile, having struck an intervening target, is tumbling significantly at the time it strikes a target, the missile’s course through the second target is much more unpredictable, both as a result of its exaggerated yawing at the point of impact and its loss of kinetic energy prior to striking the second target.
If the bullet is tumbling significantly then its yaw angle is also changing significantly. At one moment the yaw deflects the bullet in one direction and at another moment the changed yaw angle deflects the bullet in another direction. These changes are both rapid and pseudo random. So the deviation of the bullet from a straight path approximates a random walk. As a result the overall path of a significantly tumbling bullet deviates slightly from a straight path.
Alternately if the bullet strikes without tumbling and with an angle of yaw, its trajectory smoothly curves toward the direction of the long axis of the bullet. This deflection is completely predictable given the physical characteristics of the second target and the initial conditions of the second strike.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 169
(436) The panel members agree that in their experience, if a missile strikes an object capable of creating a shearing force, such as the skull, the bullet’s pathway in the body might be significantly different from the line of its trajectory prior to impact. The missile fragment lodged within the margin of the entrance skull defect is evidence of obvious shearing force with lateral torque. The only conclusion that the panel members can reach as a group is that all of the missile’s mass, small and large fragments alike, would have moved forward from the point of impact with such a bony surface. The degree of lateral movement of the pathway would be influenced by the surface’s convexity, amount of kinetic energy propelling the missile forward, and nature of the tissue through which the missile fragments were traveling.

This simplified model of the deflection problem yields general conclusions. The initial speed and hence the initial momentum of the bullet discourages the extent of the deflection in two ways. First the duration of collision is inversely proportional to the initial speed of the bullet so the changes in momentum and action are also inversely proportion to the initial speed of the bullet. Second, a larger initial momentum of a faster bullet is less affected by a given change in momentum during the collision. As rule of thumb, the deflection angle is nearly inversely proportional to square of the initial speed of the bullet.
Convexity causes the direction of the perpendicular to the surface to change from one point to another. This effect produces the illusion that convexity is related to deflection. In reality a flat, a concave or a convex surface would produce identical deflections as along as the incidence angles and striking speeds of the missiles are the same.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 169
(438) A missile's wounding capability is a consequence of the transfer of kinetic energy from the missile to the body. A missile’s kinetic energy is the same as that of any moving object: KE=mv2/2g, where m is the weight in English pounds and v is the striking velocity in feet per second. The results in conventional foot-pounds are derived by dividing by 2 times the acceleration due to gravity (32.2 feet per second per second). From this formula it can be deduced that the missile’s kinetic energy varies as the square of its velocity. Thus, doubling the velocity increases the kinetic energy by a factor of 4, while doubling the mass serves only to double the kinetic energy.
The kinetic energy of a moving body is one half times the mass multiplied by the square of the speed. In terms of the weight, the kinetic energy equals one half times the weight divided by the acceleration of gravity multiplied by the square of the speed. So the panel made two mistakes in explaining a simple equation. They incorrectly equated a speed to a velocity and incorrectly attributed the factor of one half belonging to the definition of kinetic energy to the conversion of a weight to a mass.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA 169
(439) A missile passing through a body produces, around the wound track, a hemorrhagic area composed of the tissues which have been torn by the direct impact of the bullet. The missile creates a permanent cavity, the size of which is generally proportional to the missile’s total loss of kinetic energy while in the wound. As the bullet passes through the tissue, considerable radial motion is imparted to the tissue elements and a large temporary cavity is formed. When the wound track is dissected, extensive bleeding and tissue injury may be found extending for a considerable distance away from the track produced by high velocity bullets. After sectioning the tissues, this hemorrhagic area is often well-defined; its extent is proportional to the missile's loss of kinetic energy while in the wound. High speed X-rays and motion pictures have also demonstrated the formation of this temporary cavity, with a volume that may be as much as 27 times that of the permanent cavity.
When a missile punches a hole it exerts considerable stress upon adjacent tissues not directly impacted. Although this stress decreases rapidly with distance from this punched track, the localized stress compresses vessels and pressurizes the contents. The contained fluid transmits the excess pressure along both directions of the vessel. As the vessel narrows the undiminished pressure increases the strain upon the thinning walls. Eventually the walls become too thin to constrain the pressurized fluid and the vessel ruptures. This mechanism explains how bleeding occurs within tissues at a considerable distance from the wound track.
As the speed of the missile increases so does the threshold sizes of the rupturing vessels. However, the largest distance from the wound track at which rupturing occurs is relatively independent of missile speed and is strongly dependent upon the localized details of the circulatory system.
Formation of a temporary cavity does not affect the length of the wound track. So the diameter of the temporary cavity whose volume is 27 times the volume of the permanent cavity equals the square root of 27 times the diameter of the permanent cavity. For a permanent cavity with a diameter of 6 mm or 0.236 inch, the diameter of the temporary cavity becomes 1.23 inch. Since expansion of each end of the diameter contributes toward the one-inch increase, the tissues surrounding the permanent cavity move radially outward for a distance of one-half inch before coming to a halt. This minor movement shows the slowness of the radial motion and the weakness of the driving forces.
The walls of the temporary cavity alternately move outward and inward in a series of damped oscillations. When the intervals between oscillations do not change then the motion is linear. This linearity permits calculation of the physical parameters of the motion from a few measurements. The interval between one oscillation and the next gives the damped frequency of oscillation and the ratio of one maximum amplitude to the next maximum yields the damping period. These parameters enable calculation of the natural frequency of oscillation. Finally these parameters permit calculation of the amplitude, speed and acceleration of the motion.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 170
(440) The panel agrees that the tissue disruption due to the temporary cavity created by passage of a high or intermediate velocity missile might have produced fractures of the transverse processes of one or several of the lower cervical and/or upper thoracic vertebrae in President Kennedy's neck, as indicated by the postmortem X-rays. There are significant muscle masses attached to the vertebrae which would receive tremendous shock, even if several inches distant from such a missile. A direct grazing missile impact may have occurred, but it would not have been necessary to cause the damage visible in the X-rays.
The cavity created by passage of a missile has a temporary portion since the formative stresses are insufficient to crush the quivering tissues and too weak to fracture the transverse processes. Despite the shock imparted to the muscle by the missile the stress upon the bone is limited by the adhesive strength of the tendon that attaches the muscle to the bone. The tendons spare bones from breaking by spraining first.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 170
(441) The missile's rate of energy loss in the wound and the consequent transfer of this energy to the body is dependent on several factors, including the amount of initial energy and the degree of retardation of the missile within the body. This retardation varies according to the missile's shape, the density of the tissues through which it is passing, and its degree of yaw while passing through the target.
The kinetic energy of the missile is one half times its mass multiplied by the square of its speed. So the time rate of loss of kinetic energy is calculated exactly as the speed of the missile multiplied by the retarding force multiplied by the cosine of the angle between the velocity and force vectors. This product does not depend upon the initial kinetic energy. The retarding force depends upon the dynamic yield strength of the tissues and the striking or displacement area of the missile. This latter factor is a function of the shape and yaw angle.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 170
(442) The changes in density from air to skin, muscle, and bone may produce marked variations in yaw. A bullet that is positioned appropriately relative to its trajectory on penetrating the skin may be tipped 90(deg) to 100(deg) within 3 inches of penetration, thus dramatically reducing speed, with a corresponding increase in energy transfer and tissue destruction. Subsequently its posture may again change, so that its long axis is in the line of flight and considerably less energy is lost and consequent tissue damage is minimized.
A density boundary will exert a torque upon a tangentially incident bullet. This torque arises with the first contact between the bullet and the boundary, continues while the bullet is crossing and ceases when the bullet clears the boundary. During this interval the bullet experiences angular acceleration. The bullet clears the boundary with an acquired angular speed equal to the angular acceleration multiplied by the duration of the interval. In turn this duration equals the distance traveled during the tangential crossing of the boundary divided by the linear speed of the bullet. So the angular speed gained by the bullet from a tangential crossing of a density boundary is inversely proportional to the linear speed of the bullet. The change of yaw angle as the bullet clears the boundary equals one half the acquired angular speed multiplied by the duration of the crossing. Since this duration is inversely proportional to linear speed of the bullet, the change of yaw angle is inversely proportional to the square of the linear speed.
An imaginary clock with a bullet moving toward twelve o’clock illustrates the effect of speed upon the change of yaw angle. Suppose a target causes the long axis of the bullet moving at 500 foot per second to point toward three o’clock after a three-inch penetration. Changing the speed of the bullet to 1936 foot per second while keeping other variables constant would result in the long axis of this faster bullet pointing one-fifth the arc between twelve and one o’clock. This mental experiment dramatically illustrates that marked variations of yaw angle is a characteristic of a slow bullet.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 171
(445) The effects of a missile striking a portion of the body will conform to the basic laws of motion, readily understood and often observed in everyday occurrences such as the collision of a moving with a stationary billiard ball. If the two balls are of equal mass and the energy of the first is transmitted on impact to the second, the first ball will stop completely, while the second will be propelled at a velocity comparable to the striking velocity of the first.
If the first billiard ball imparted all of its kinetic energy to the second billiard ball then this would permit the second ball to transfer all of its kinetic energy during a collision with a third billiard ball and thus reveal the possibility of a never-ending chain of lossless collisions. This violation of the law prohibiting a perpetual motion machine arises from the false assumption that a billiard ball can transfer all of its kinetic energy to another ball.
The proper solution of the problem recognizes that the initially stationary ball gains a kinetic energy that is a fraction, f, of the kinetic energy lost by the initially moving ball. Let V0 be the initial speed of the moving ball, V1 be its final speed and V2 be the final speed of the formerly stationary ball. Symbolically the partitions of kinetic energies give the relationship
|
|
|
|
Post by Herbert Blenner on Feb 11, 2019 15:22:41 GMT -5
f ( 0.5 m V02 - 0.5 m V12 ) = 0.5 m V22,
where m is the common mass of the billiard balls. Conservation of momentum requires
m ( V0 - V1 ) = m V2.
Solving these equations yield
V1 = V0 ( 1 - f ) / ( 1 + f ) and V2 = V0 [ 2f / ( 1 + f ) ].
These solutions show that stoppage of the first ball, V1 = 0, infers the forbidden case of f = 1 for which V2 = V0.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 171
(445) . . . If the second ball is twice the mass of the first and the transmitted kinetic energy is comparable to that of the first, it will be propelled forward at only half the velocity. Much of the kinetic energy transferred by the first ball is due to its velocity, since its mass, relative to that of the second ball, is insignificant. Nevertheless, the sum of mass and velocity will result in significant imparted velocity to the motionless target.
The conclusion that the second ball will be propelled at the initial velocity of the first does not follow from the assumed transmittal of kinetic energy. A proper application of the panels improper use of kinetic energy conservation gives the velocity of the second ball as the velocity of the first divided by the square root of two. Ironically applying the correct principle of momentum conservation shows that the second ball of twice the mass of the first acquirers one half the velocity lost by the first ball. Using the stipulation that the collision stops the first ball gives the reported result that the second ball will be propelled at half the initial velocity of the first ball.
When the stationary ball has twice the mass of the moving ball the condition for the kinetic energies becomes
f ( 0.5 m V02 - 0.5 m V12 ) = m V22
Applying momentum conservation gives
m ( V0 - V1 ) = 2m V2.
Solving these equations yield
V1 = V0 ( 1 - 2f ) / ( 1 + 2f ) and V2 = V0 [ 2f / ( 1 + 2f ) ].
The conclusion that the second ball of twice the mass will be propelled at half the initial speed of the first does not follow from the assumed transmittal of kinetic energy.
0.5 ( 2m ) V22 = 0.5 m V02
A proper solution of the panel’s improper method gives the speed of the second ball as the initial speed of the first ball divided by the square root of two.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 171
(446) This situation can be best observed using non jacketed missiles designed to impart maximum transfer of kinetic energy to the target during and after striking, thereby maximizing the missile's "knockdown" capability and minimizing the possibility of exit from the target and the striking of a second target. A jacketed missile transfers significant, but considerably less, kinetic energy to the target. Instead, the energy transfer propels the target body or a portion of it in the same direction as the missile. The vector of propulsion might affect the body in its entirety if the victim were standing, or might affect only the upper portion of the body if the victim were seated depending on the site of impact. The movement of the body, or of a large portion of it, will be minimal because of the bullet's small mass, not withstanding its high velocity. If the bullet strikes the head, an object of relatively low mass in comparison with the entire body, the movement of the head in the direction of missile travel may be considerable. Rotational movement of the head, or of a lightweight portion of the body may also occur.
A transfer of momentum from the missile does not propel the body or the struck portion in the same direction as the missile. This situation arises since neither the body nor its struck portion is free from the deflecting influence of non ballistic forces. In particular if a bullet strikes the head then the forces arising from the attachment of the head to the neck would deflect the motion of the head from the direction of the striking bullet. So a rotational movement of the head would always occur in response to the striking bullet.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 171
(447) . . . In cases where the body was in a supported position that would preclude motion, such as lying against a firm surface, a transfer of kinetic energy from the missile to the body will result but not cause motion. Transmission of such energy to the body will be manifest by injury to areas in contact with the supporting surfaces.
As the missile approaches exit from the body, it exerts a force that accelerates the surrounding tissues. The preclusion of motion of the body infers that an equal and opposite force from the firm surface canceled the force from the missile. Under these conditions the tissues near the surface experience approximately twice the force arising from the missile alone. When the area of contact is small compared with the area of the body then the stress from the equal and opposite force is increased many fold and explains the injury to those areas in contact with the supporting surface.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 173
(453) Another consideration about missile wounds that has been emphasized by others is the relatively short time that a missile is actually moving through tissue, usually less than a thousandth of a second. A bullet of 150 grains weight, passing through 8 inches of tissue, entering at 2,000 feet per second (approximately the velocity of the 6.5 millimeter Mannlicher-Carcano bullet) and exiting at 1,000 feet per second will pass through the body in 0.00045 second and impart to the tissue 998 foot-pounds of energy, the work equivalent of more than 4,100 horse power. This energy transfer produces a temporary cavity as described earlier, which actually develops after the bullet has passed through the tissue. Accordingly, a bullet can pass through a head and be about 100 feet further along before a photograph reveals the explosive destruction of the head. This also explains the presence of entry and exit bullet holes in bones and tissue even though the skull is extensively fragmented or blown apart by the subsequent formation of the temporary cavity. The velocity of the outward-moving tissue particles may be only 125 feet per second, far less than the 1,000 to 2,000 feet per second velocity of the bullet projectile. Thus, when the Zapruder film reveals the explosion of the skull, the bullet had already passed through.
The tissue did 998 foot-pound of work in slowing the missile from 2000 foot per second to 1000 foot per second and converted practically all of the 998 foot-pound of the kinetic energy lost by the missile into thermal energy known as heat. Conservation of momentum describes the transfer of kinetic energy from the missile to the head. Calculations show that the kinetic energy transferred to the head equals one-third of the mass of the missile divided by the mass of the head multiplied by the kinetic energy lost by the missile. The factor of one-third arises from the difference of the entry and exit speeds divided by the sum of these speeds. For a 0.0214-pound missile and a 10-pound head the transferred kinetic energy is 0.71 foot-pound. If this kinetic energy were equally shared between the rotational forward nod of Kennedy's head and the ejected matter then weight of the ejectra based upon the specified speed of 125 foot per second becomes 0.0015 pound, less than 1/42 ounce. Without doubt, the panel has not explained the ejection of matter seen on the Zapruder film.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 173
(455) The panel members agree that the exit wound of a missile seriously deformed by initial penetration of the skull might be considerably larger than the entrance defect and that the forces related to yaw and the large temporary cavity created by the missile would usually be transmitted fairly equally throughout a closed space such as the skull. The larger exit defect in the front of the skull would theoretically permit greater exodus of tissue under pressure, and a resulting backward movement of the head could occur.
The forces from the transiting bullet would be equally distributed within the liquids in the head while solids such as tissues would constrain forces to the immediate vicinity of the missile. An exodus of tissue under pressure would have no effect upon the movement of the head. Instead an opening prevents a pressurized liquid in its immediate vicinity from exerting a balancing force upon the missing skull that would cancel the force in the opposite direction upon the tissue or the skull. This situation produces a jet effect. However, since liquids are nearly incompressible, the slightest expansion of the containing volume or escape of liquid through a hole relaxes the pressure. So the extreme briefness of the jet effect renders the induced motion as practically immeasurable.
Elastic contraction of the container can substantially extend the duration of the jet and produce significant motion. This effect describes the flight of a deflating balloon. The thrust begins with the initial escape of the contained liquid or gas and continues until the container ruptures of its contraction ceases.
Source: Summary of the Forensic Pathologists’ Perspective of Wound Ballistics - 7HSCA, 174
(459) The panel concludes that the backward movement of the head following its forward movement occurred after the missile had already exited from the body and had created a large exit defect in the skull, and that it was most probably due to a reverse jet effect, or a neuromuscular reaction, or a combination of the two. The short interval between the two motions supports this explanation.
The backward movement of the head began long after fracturing of the skull converted stored elastic energy that had potential to drive a balloon effect into a form of energy incompatible with a jet effect.
Appendix One
A target gains kinetic energy from a bullet by transfer of momentum. In particular, the target gains precisely the momentum lost by the bullet. A numerical example shows that the panel’s idea of transfer of kinetic energy predicts unreasonable results. Suppose a target of mass, M, initially at rest and suspended by a long string stops a bullet of mass, m, moving horizontally with a speed of v. Conservation of momentum yields
m v = ( M + m ) V,
where V is the speed of the target at the instant that the bullet stops. Solving for the instantaneous speed of the target gives
V = v / ( M / m + 1 ).
Taking the mass of the target as 10 pound / g, the mass of the bullet as 0.023 pound / g and its striking speed as 1900 fps gives the instantaneous speed of the target as
V = 1900 fps / ( 10 / 0.023 + 1) = 4.36 fps.
Using the panel’s incorrect idea of kinetic energy transfer gives the relationship
0.5 m v2 = 0.5 ( M + m ) V2.
Solving the instantaneous speed of the target gives
V = v / ( M / m + 1 )1/2.
Using the same values for the variables, transference of kinetic energy predicts an instantaneous speed of
V = 1900 fps / ( 10 / 0.023 + 1 )1/2 = 91.0 fps.
External forces govern the target after being set into motion by the bullet. In this case raising against the force of gravity consumes kinetic energy. The target stops when it reaches a height h where its increase in potential energy equals the instantaneous value of kinetic energy acquired by transference of momentum.
( M + m ) g h = 0.5 ( M + m ) V2
Noting that the common factor of the sum of masses cancel gives
h = V2 / ( 2 g ).
The arc distance traveled by the target, S, equals the length of the string, L, multiplied by the angle between the string at stoppage and the vertical. The cosine of this angle equals ( L - h ) / L. Combining results yields the desired expression for S.
S = L arccos ( 1 - V2 / [ 2 g L ] )
This result shows that a bullet imparts a speed to a target and non ballistic forces govern the subsequent movement.
|
|










