|
|
Post by Herbert Blenner on Feb 11, 2019 14:57:35 GMT -5
Modulation Mattersby Herbert Blenner | Posted October 5, 2012 Understanding the acoustic evidence requires a working knowledge of several electronic concepts. These concepts are amplitude, frequency, signal, modulation, carrier, automatic gain/volume control, saturation, limiter, noise immunity, beating, heterodyne and peak detector
Amplitude abstracts the familiar concepts of loudness as a measure of sound or brightness as a measure of light. Likewise the abstraction of frequency unifies the concepts of pitch of sound or color of light.
Sound and light convey information. In this sense sound and light are two different types of signals. The changes in loudness or pitch of sound or the changes in brightness or color of light are modulations of the signals that convey information.
Amplitude Modulation, AM, conveys information by changing the loudness of sound, the brightness of light or the amplitude of a radio signal. Likewise Frequency Modulation, FM, conveys information by changing the pitch of sound, the color of light or the frequency of a radio signal. The familiar red, yellow and green traffic lights are an example of the use of frequency modulation to convey information to motorists.
AM and FM radio receivers extract information from radio signals known as carriers. These signals carry information by amplitude modulation or by frequency modulation. The type of modulation determines the components of the receiver and how they work.
A scale with a capacity of ten pounds cannot distinguish a twelve-pound weight from a fifteen-pound weight. Likewise an AM receiver cannot distinguish amplitude changes in a signal whose levels exceed the capacity of its components. For this reason, AM receivers use automatic gain control, AGC, circuits to prevent the amplitudes of signals from exceeding the capacity, known as the saturation level, of its components.
FM receivers do not use AGC to prevent the loss of information carried by amplitude modulation. In fact, FM receivers use a limiter stage designed to saturate. This limiter provides noise immunity to random changes in amplitude, a benefit that justifies the complexity and increased cost of a FM receiver. However, the RF amplifier uses AGC to improve image rejection of unwanted signals.
A simultaneous playing of the same note on two musical instruments exhibits beating. Although both notes have slowing diminishing loudness, the composite sound has oscillating changes in amplitude unless the instruments are exactly tuned to the same note.
Likewise simultaneously received radio carriers beat within an AM or a FM radio. In both cases the beat frequency is half the difference of the carrier frequencies. This beating is strongest when the amplitudes of the carriers are equal. When the amplitudes of the carriers are unequal then the weaker carrier determines the amplitude of the beat.
An AM receiver responds to the beating of signals by producing a continuous and periodic tone known as a heterodyne. When the carriers have equal amplitudes, the heterodyne has a maximum amplitude comparable with the amplitude of a fully modulated signal. In general this level would not activate the automatic volume control, AVC, circuit of the audio stage.
Ideally the carrier frequencies of AM transmitters are constant. If one transmitter has a frequency of 151,782 kHz and another with a frequency of 151,780 kHz comes on the channel, then the carriers produce a beat frequency equal to half the difference of the carrier frequencies. This yields a 1-kHz beat frequency of the composite signal. The heterodyne frequency would not vary with the amplitude modulation of either carrier. In practical systems they tolerate a small initial drift in the frequency of a transmitter. Hence the frequency of a heterodyne may begin with a slight change in frequency before becoming constant.
The response of a FM receiver to beating carriers is more complicated than the response of an AM receiver. When the carriers have nearly the same amplitude then the beating causes the composite amplitude to alternately fall below and rise above the saturation levels of the limiter. This causes a heterodyne when the composite amplitude is between the two saturation levels which ceases when the composite amplitude exceeds either saturation limit. So a FM receiver produces a discontinuous and periodic heterodyne that alternately switches on and off. These changes increase the harmonic content and reduce the average power of the heterodyne as compared to an AM receiver.
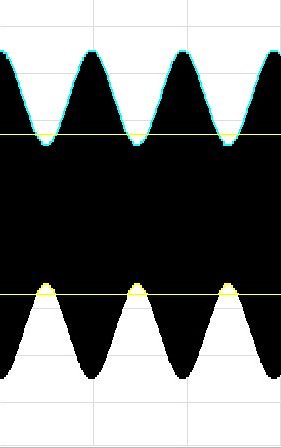
Figure 1 - Heterodyne From a FM Receiver
Figure 1 shows beating of two sinusoids where the amplitude of the stronger carrier is 2.5 times the amplitude of the weaker carrier. Under these conditions the light blue curve represents the waveform of the heterodyne produced by an AM receiver.
The yellow horizontal lines on these figures represent the saturation levels of the limiter. An FM receiver would produce a heterodyne tone only when the peaks of the composite signal fall between the saturation levels. For this case the lower yellow line with small sinusoidal peaks represent the discontinuous waveform of the heterodyne.
Practical FM receives have a threshold for the difference of carrier amplitudes for production of a heterodyne. When the difference exceeds this threshold, the amplitudes of the beats become too small to drive the limiter out of saturation. Under these conditions the beating carriers do not produce a heterodyne.
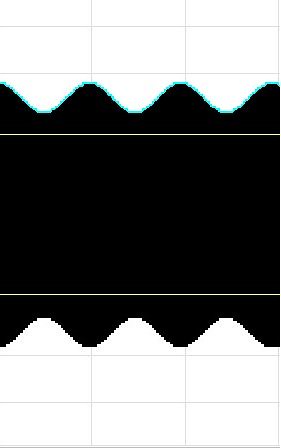
Figure 2 - No Heterodyne From a FM Receiver
In the simulation of figure 2, the amplitude of the stronger carrier is 8.0 times the amplitude of the weaker carrier. This factor is notably small in a radio repeater environment where signals have a thousandfold variation of their amplitudes.
Further a FM receiver intended for network operation had the option of using a ratio detector that has heterodyne rejection instead of a Foster-Seeley detector. The cost of this improvement was less than one dollar for two resistors and one capacitor.
In a FM system the carrier frequency of a modulated transmitter changes rapidly. Suppose a station has a nominal frequency of 151,783 kHz and audio causes a frequency deviation of 1 kHz. This means that the instantaneous frequency of the station varies from 151,782 to 151,784 kHz. If an unmodulated station with a nominal frequency of 151,780 kHz comes on the channel, it will produce a composite signal whose beat frequency varies between 1 kHz and 2 kHz. Under these conditions the ear would hear a loud hissing noise, instead of a tone.
|
|
|
|
Post by Herbert Blenner on Feb 11, 2019 15:03:13 GMT -5
In an article, Signal Processing Analysis of the Kennedy Assassination Tapes, published in Science & Society, the Watson Research Center of IBM presented a highly significant discussion of heterodynes, AGC and brieftones on the Bowles tapes of the Dictabelt and the Audograph disk. In short they described how signals would have behaved if processed by an AM receiver.
Fortunately, the center provided sufficient details to test their reported observations. I quote IBM.
Channel-I Heterodynes
On Channel-I spectra, several narrow-band high-energy tones are intermittently present for short durations. These tones are not on Channel II. Also at the end of each tone. [sic] there is evident a sharp drop in total Channel-I energy. This indicates some kind of AGC (Automatic Gain Control) action.
These narrow-band tones are called heterodynes. They were generated when another transmitter came on the radio channel, while the transmitter with the stuck-open mike was transmitting. The difference in their carrier frequencies resulted in the heterodynes.
Unlike speech, the loud interference on Channel-I had no silent intervals between words. Instead the buzzing noise produced a continuous frequency modulation of the carrier. Under these conditions the many observations of "narrow-band" heterodyne tones require that a silent station was transmitting an unmodulated carrier when "another transmitter came on the radio channel" with its unmodulated carrier and produced a narrow-band heterodyne with unchanging frequency. Two unmodulated stations are necessary for generation of a narrow-band heterodyne in the FM receiver used by Channel-I. Clearly the invention of a second stuck-open transmitter to explain the many narrow-band heterodyne tones is an untenable explanation.
If the second carrier is strong.[sic] it should also activate the AGC action in the IF (Intermediate Frequency) stage of the radio receiver.
Channel-I AGC
Most radio receivers have an AGC circuit at IF stage to maintain a steady IF signal level at the detector or discriminator. If there is a sudden increase in the RF signal (such as caused by switching on a strong carrier). AGC acts rapidly to reduce the IF amplifier gain to bring down the signal within acceptable limits. On the other hand if there is sudden decrease (such as caused by switching off a strong carrier) in the RF signal level, AGC acts more slowly to restore the IF amplifier gain. This is a typical characteristics [sic] of an AGC circuit: fast attenuation and slow recovery. The AGC action also affects the audio output level because of the drop in overall gain of the system. Therefore, when a heterodyne begins, we should expect a sudden drop in the recorded level of the signal picked up by the stuck-open mike. And after the heterodyne ends, we should expect a slow recovery in the audio signal to its original level. This phenomenon is indeed observed in Channel-I spectra.
All radio receivers with AGC action at their IF amplifiers are designed for reception of AM whereas a FM receiver does not use AGC at the IF amplifiers. This is the lesser problem with the preceding paragraph. The upper oscillograph of figure 3 shows a heterodyne between the red markers. This signal on trackone0162 appears to begin with a fast attenuation and a slow recovery after the heterodyne ends.
|
|
|
|
Post by Herbert Blenner on Feb 11, 2019 15:04:20 GMT -5
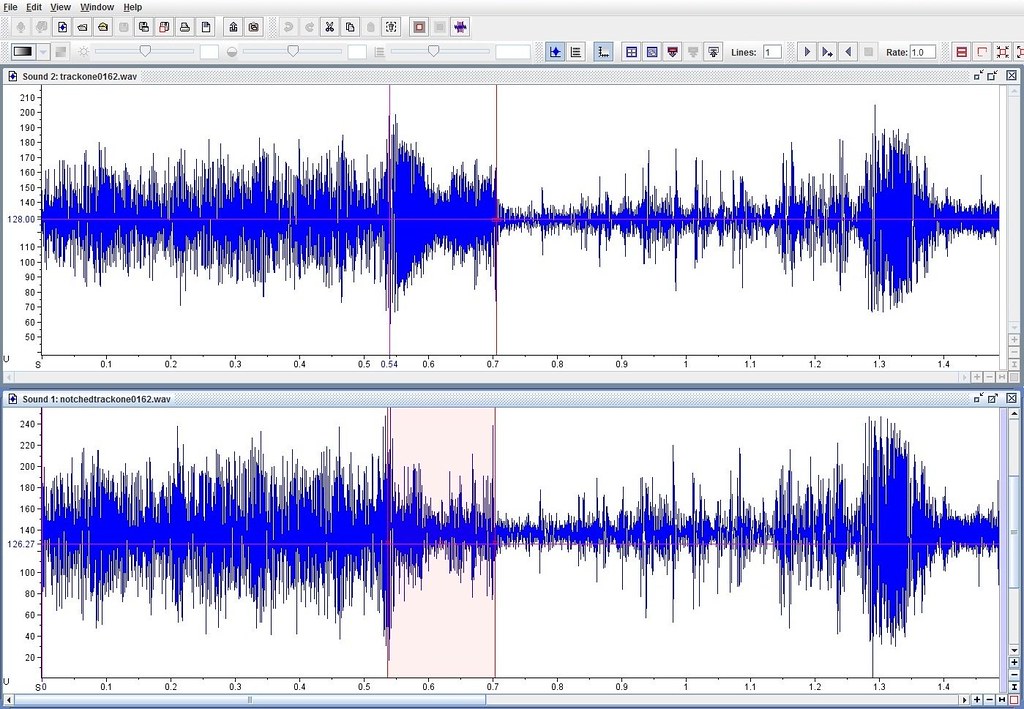
Figure 3 - Slow Recovery Without Fast Attenuation of Uncovered Signal
A pink background on the lower oscillograph of notchedtrackone0162 highlights the signal uncovered by filtering the narrow-band heterodyne. Instead of a fast attenuation of the uncovered signal, the notch filter reveals changes indifferent to the monotonic decrease of gain due to fast AGC attenuation. Since fast attenuation acts upon all frequencies equally, this behavior of the uncovered signal excludes AGC as the cause of the apparent fast attenuation of the heterodyne.
If the AGC action occurred at the audio stages of the Dictaphone or along the telephone line that connected the dictaphone to the FM receiver in Fair Park then the effect upon the uncovered signal would be the same. In particular true AGC action would equally attenuate the heterodyne and the underlying signal.
Since recovery from fading would not affect the volume of a signal recorded from a FM receiver, this slow recovery from a nonexistent fast attenuation presents a serious dilemma.
If the Channel-II cross-talk was indeed picked up by the stuck-open mike, its level should change to reflect Channel-I receiver AGC action. To test this hypothesis, we estimate the level of cross-talk as a function of time and compare with timing of Channel-I heterodynes. Before we look at it quantitatively, let us examine the spectra again.
A comparison of the oscillographs of another heterodyne with the underlying signal exposed by filtering shows that the absence of the fast attenuation preceding the slow recovery is part of a pattern rather than an exception to the rule.
The upper oscillograph of figure 4 shows a heterodyne that begins at 0.83 second from the start of trackone0157 and ends at 0.98 second. During this 0.15-second interval the amplitude of the heterodyne decreases with a shape reminiscent of the exponential envelope expected from attenuation by AGC action. Further the time constant of this decrease being in the vicinity of tens of milliseconds is typical of the fast attenuation of AGC action.
Both oscillographs show a gradually increase of the background signal after the heterodyne ceases. The rate of this increase is consistent with the slow recovery of AGC action. |
|
|
|
Post by Herbert Blenner on Feb 11, 2019 15:05:25 GMT -5
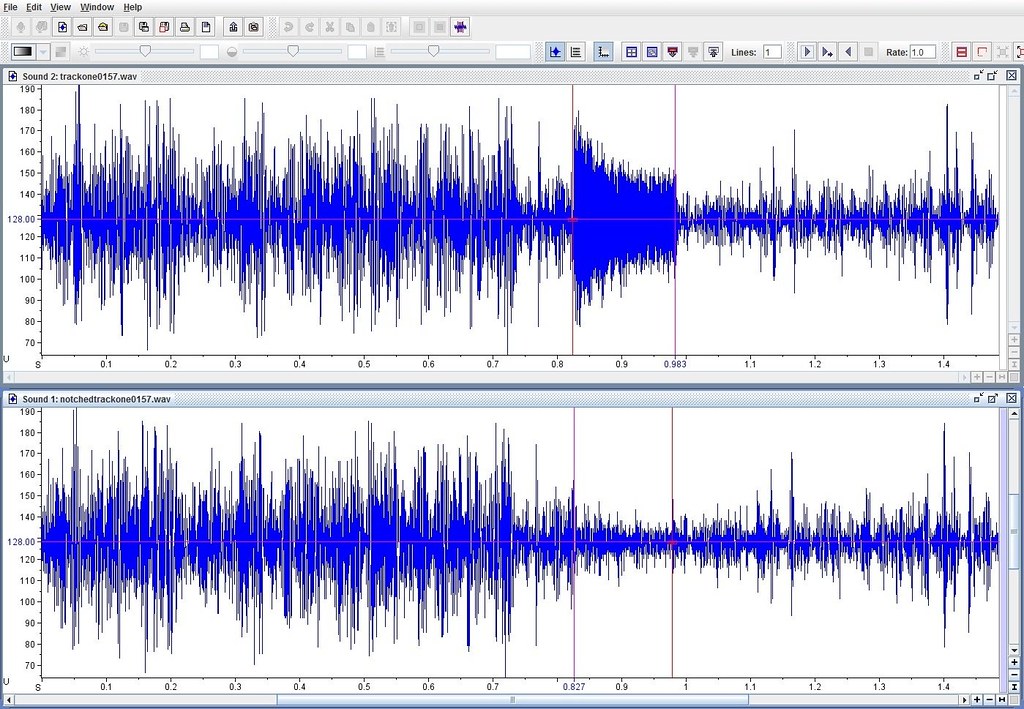
Figure 4 - Another False AGC Signature
On the upper oscillograph, the red lines mark the starting and ending times of the heterodyne. The lines on the lower oscillograph of notchedtrackone0157 mark the signal exposed by filtering the heterodyne. Instead of seeing an exponentially decreasing signal attenuated by the same factor as the heterodyne, the notch filter reveals a nearly constant signal envelope.
The dilemma of a slow recovery from a nonexistent fast attenuation is confirmed.
Channel-II Brieftones
On Channel-II spectra (Figs. [3, 4 and 5]) we note that during voice transmissions there are no silence gaps between words. The signal level of Channel II is fairly constant. This could result from the presence of nearby motorcycle radios tuned to Channel II, while someone is transmitting on Channel II. A radio receiver close to a transmitting mike could form a closed loop having greater than unity gain. This will excite a natural frequency of the loop and it will act as an oscillator. The resulting oscillations will be recorded on the Channel-II recorder. We notice this phenomenon on Channel-II recording. During these periods, the spectra consist of a strong sinusoid (in the frequency range 1300-1800 Hz) and its harmonics. There is virtually no other signal present during these periods. We call these "Brieftones." Being high energy and very narrow-band, these are extremely valuable in determining the cross-talk level. On Channel II spectra (in Figures 4(b) and 5(b)) I[sic] second harmonics of brieftones are quite prominent, while on Channel I spectra, all the Channel-II brieftones are present but their harmonics are not visible, indicating the limited frequency range of Channel I (even in the normal recording of Channel-I communications, the Channel-I recording has a similar roll-off at high frequencies.).
A brieftone is an oscillation caused by acoustic coupling between a transmitter and receiver linked by radio waves. This coupling forms a feedback loop containing the linked transmitter and receiver. Although one transmitter and one receiver initiate this brieftone, the repeater sends this loud oscillation to every receiver on the channel.
Circuits of AM and FM receivers operate to ensure that the brieftone has equal negative and positive portions. This asymmetry suppresses the even harmonics of the brieftone. So the spectrum of a narrow-band brieftone consists of a fundamental frequency and its odd harmonics.
The significant intermodulation distortion of Channel-II audio compressor circuits caused all signals to have prominent second harmonics and generated second harmonics of the brieftones.
Now we discuss implications of these plots. We shall begin with the "Pre-Stemmons" phrase (Figure 7). During this phrase, T(t) is generally increasing reaching a value of about 7 dB before the Channel-I heterodyne begins at 7.91 seconds (Channel-I time). For the next Channel-II brieftone (from 3.90 to 4.16 seconds, Channel-II time), T(t) is around -10 dB; a drop of 17 dB. This Channel-II brieftone is clearly visible on Channel-I spectra (Figure 4(a)), although greatly attenuated. This is a clear indication of the effect of Channel-I AGC (due to a Channel-I heterodyne) on the cross-talk level. This also indicates that the Channel-II cross-talk was already present in Channel-I signal when it was being received by the Channel-I radio receiver/recorder. In the other two phrases also we find similar indications of cross-talk being received over the radio. This rules out the possibility of it being superimposed later acoustically or electrically.
The argument that rules out superimposition of the crosstalk is dependent upon the loudness of a Channel-I heterodyne causing the AGC to reduce the level of crosstalk. The first and an exceptionally loud heterodyne on trackone01300131 permits testing this necessary interaction between the loud heterodyne and the overall gain of Channel-I, not just the gain of the IF amplifiers.
The upper oscillograph of figure 5 shows the exceptionally strong heterodyne between the red vertical line. Despite loudness, the envelope of this heterodyne shows no evidence of fast attenuation. The region to the right of the right line reveals no evidence of slow recovery since the weaker heterodynes which followed in rapid succession have equal amplitudes. So both characteristics of AGC action are absent.
|
|
|
|
Post by Herbert Blenner on Feb 11, 2019 15:06:09 GMT -5

Figure 5 - No AGC Action With An Exceptionally Loud Heterodyne
On the lower oscillograph of notchedtrackone01300131, the red lines mark the region in which a notch filter removed the fundamental frequency of this exceptional heterodyne. The uncovered signal exposed by the notch filter reveals an abrupt decrease in level which coincided with the start of the heterodyne. This behavior is expected in a FM receiver where the unmodulated carrier reduced the net frequency deviation of the composite signal. Since the audio level is proportional to the frequency deviation, switching on an unmodulated carrier causes an abrupt reduction of the volume.
Next, we examine the "Stemmons" phrase (Figure 8). In this segment, a Channel-I heterodyne ends (at 21.23 seconds, Channel-I time) just before the Channel-II communication begins (at 14.18 seconds, Channel-II time). During the first Channel-II brief tone (14.25 to 14.51 seconds, Channel-II time), T(t) function is increasing rapidly, registering a gain of about 10 dB. This indicates recovery of Channel-I AGC at the end of the heterodyne. There is a brief Channel-I heterodyne from 22.41 to 22.49 seconds, Channel-I time). This heterodyne is different from others in that it is around 1200 Hz while others are around 2500 Hz. Nevertheless, this heterodyne also activates the Channel-I AGC which is evident from the total Channel-I energy plot as well as the T(t) plot. Following this heterodyne the recovery is slow, taking about a second or so. There is another Channel-I heterodyne from 25.81 to 26.30 seconds, Channel-I time. A Channel-II brieftone was already present when this heterodyne began. The dramatic effect of Channel-I AGC, due to the heterodyne, is evident in T(t) plot which drops by more than 15 dB over a very short period. This is also clear on Figure 5(a) where the intensity of the Channel-II brief tone dramatically reduces as soon as the Channel-I heterodyne begins.
Exceptionally strong heterodynes have other functions. They appear on the Bowles tape of the Dictabelt, track one, and the hum corrected copy of this tape, track five. The heterodynes have sufficient strength to enable accurate measurements of their durations, frequencies and number of contained cycles. These measures produced truly dramatic results.
Although they played a portion of track one at a reduced speed to tape the hum corrected copy, the frequencies of the corresponding heterodynes have a ratio of 0.9984. However, intervals between events require that the frequency ratio of these heterodynes should by 0.9768. This discrepancy is overwhelmingly strong evidence that these heterodynes were not present when the FBI taped a playing of track one at reduced speed to make the hum corrected copy of track five. This work is presented on the web page, Five to One.
Dramatic conclusions demand corroboration. The exceptional heterodyne on trackone02180219 provides more than necessary confirmation.
The heterodyne between the red lines of the upper oscillograph of figure 6 shows a suggestion of fast attenuation and a pronounced slow recovery. However, the lower oscillograph of notchedtrackone02180219 after filtering of the heterodyne shows an abrupt decrease in level when the heterodyne ceased and no evidence of fast attenuation at the beginning of the heterodyne. Both changes are inconsistent with action of AGC. |
|
|
|
Post by Herbert Blenner on Feb 11, 2019 15:06:48 GMT -5

Figure 6 - Abrupt Decrease of Channel-I Signal With Cessation of the Heterodyne
A comparison of this heterodyne on track one with its counterpart on track five produces devastating results. As before the frequencies of the heterodynes are nearly equal with a ratio 0.9998 whereas the timing of other events demand a ratio of 0.97139. But now the durations of the heterodynes scale in accordance the ratio based upon timing of events. As a result, the number of cycles contained by these heterodynes differ significantly from one tape to the other. The strong evidence of heterodynes being added to the acoustic records after the FBI made their hum corrected copy has passed into the category of proof.
Appendix 1 - Block Diagrams of Radio Receivers
A block diagram shows the main components of an electronic system. This presentation illustrates the relationships between the various components without unnecessary details.
AM and FM receivers use the same tuner principle to select one radio station and reject other stations on different frequencies within the same band. These receivers use a radio frequency, RF, amplifier, an adjustable local oscillator and a mixer to convert the frequency of a desirable station to the fixed intermediate frequency, IF, for further processing.
Tuners for AM or FM use an antenna driven radio frequency, RF, amplifier whose gain is regulated by an AGC circuit. The output of this RF amplifier connects to a mixer which is also connected to a local oscillator whose frequency is adjustable. The mixer multiplies one input signal by the other and produces signals of new frequencies that are the sum and the difference of the frequencies of the two input signals. Since the frequency of the local oscillator is adjustable the mixer selects different radio frequencies for processing by the intermediate frequency, IF, amplifier. Appendix 2 derives an expression for the product of sinusoids with differing frequencies. |
|
|
|
Post by Herbert Blenner on Feb 11, 2019 15:07:31 GMT -5
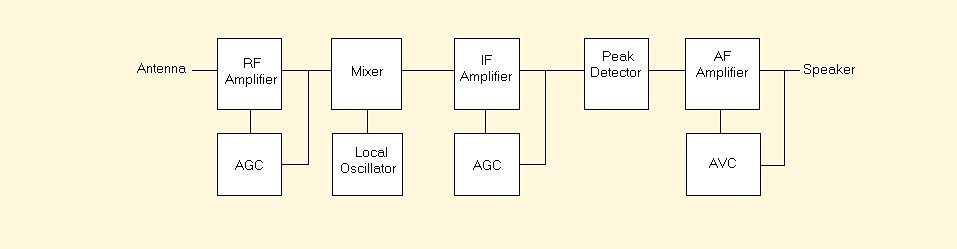
Figure 7 - Block Diagram of an AM Radio Receiver
For example, if the fixed IF frequency is 10.7 mHz then setting the local oscillator to 139.7 mHz select stations with frequencies 129.0 mHz and 150.4 mHz for reception. Practical receivers use a frequency-tunable filter in the RF amplifier to enhance one station while reducing the other station.
The IF amplifiers of AM receivers differ substantially from the IF amplifiers of FM receivers. For AM receivers, IF amplifiers have moderate gain controlled by an AGC circuit to prevent saturation by stronger signals. By contrast the IF amplifiers of FM receivers have high gain unregulated by an AGC circuit to drive a limiter stage into saturation.
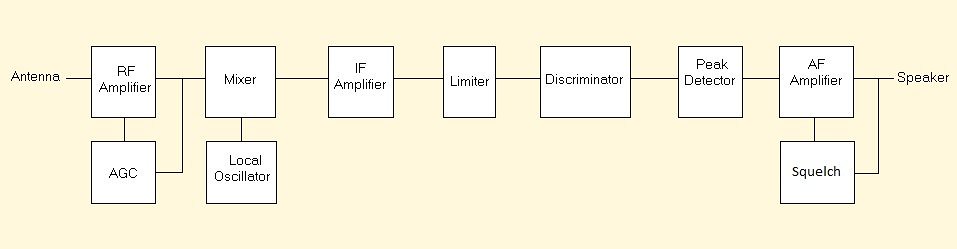
Figure 8 - Block Diagram of a FM Radio Receiver
Likewise the detector stage recovers the modulated information from the radio carrier is simpler for AM than for FM. Typically the AM receiver uses one diode, one resistor and one capacitor to implement a peak detector. These three parts that are also used by a FM receiver cost less than one dollar. However, the FM receiver requires a discriminator that converts the saturated frequency modulated signal to an unsaturated amplitude modulated signal. This additional step enables the simple peak detector to recover the modulating signal from the FM carrier.
Finally, AM and FM receivers use different schemes to control gain of their audio frequency, AF, amplifiers. In an AM receiver, an automatic volume control, AVC, circuit adjusts gain of the AF amplifier. FM receives use a squelch circuit which controls gain of the AF amplifier by turning it off or on. This action is necessary to squelch the loud noise produced by the high gain of the IF amplifier in the absence of a radio carrier to produce saturation.
Appendix 2 - The Product of Sinusoids of Differing Frequencies
Replacing X = At and Y = Bt in the familiar trigonometric identity for the cosine of the sum of two angles, X and Y, yields the corresponding identity for the cosine of the sum of two frequencies, A and B.
Cos ( At + Bt ) = Cos ( At ) Cos ( Bt ) - Sin ( At ) Sin ( Bt ) (1) Substituting Bt = - Bt in equation one yields an expression for the cosine of the difference of two frequencies. Cos ( At - Bt ) = Cos ( At ) Cos ( Bt ) + Sin ( At ) Sin ( Bt ) (2) Adding equations one and two enables solving for the product of cosines whose arguments have differing frequencies. Cos ( At ) Cos ( Bt) = 1/2 [ Cos ( At + Bt ) + Cos ( At - Bt ) ] (3) |
|











